【Excel】IFS関数をIF関数で代用するには？

IFS関数はExcel2016から追加された新しい関数で、IF関数の条件を複数に出来る関数です。いったいどの程度便利なのかを調べてみます。
また、今回はIF関数で代用する方法についても確認していきます。

IFS関数の利便性

一番重要なのはIFS関数はExcel2016から追加された新しい関数であるという事で、Excel2013以前のバージョンではIFS関数は使用できません。
(いったい何割の会社がExcel2016で業務出来ているのかという話なんですが…)

IFS関数は

IFS(論理式①,①に一致する場合,論理式②,②に一致する場合,…）

という形の数式になり、論理式自体は最大127個まで追加できるとのことです。
実際の使用方法について見てみましょう。

例題：模試結果と合格判定を5段階評価
模試の点数によってA~E判定を付けていきます。

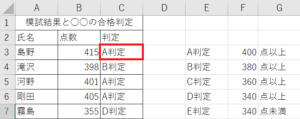
=IFS(B3>=F$3,E$3,B3>=F$4,E$4,B3>=F$5,E$5,B3>=F$6,E$6,B3<F$7,E$7)
=IFS(B3が400以上ならA,B3が380以上ならB,B3が360以上ならC,B3が340以上ならD,B3が340未満ならEの判定)

たしかに複数条件を1つの関数でまとめることができているので、複数の関数名が出てくるよりかは見やすいです。

IF関数での代用と欠点

ただ、やはりExcel2013以前のバージョンの場合でも使用したいケースも多々あります。
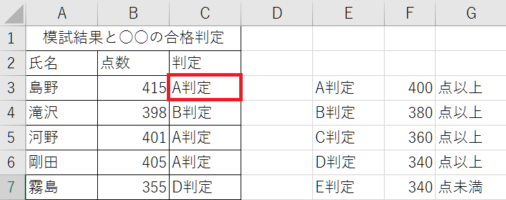
先程の例と同じものを見てみます。

IF関数で表す場合には、

=IF(B3>=$F$3,$E$3,IF(B3>=$F$4,$E$4,IF(B3>=$F$5,$E$5,IF(B3>=$F$6,$E$6,E7))))
=IF(B3が400以上ならA,IF(B3が380以上ならB,IF(B3が360以上ならC,IF(B3が340以上ならD,そうでなければE))))

そこまで大差なく表すことができます。注意すべきは最後の2つの条件(DとE)が残った段階で真ならD、偽ならEとしないと関数が終われません。
IF関数内にIF関数が出てくる(ネストといいます)ので今どこについての話なのかをよく整理していきましょう。

IFS関数について

1つの関数で済む
条件分岐が127までいける

Excel2013以前は対応していない

IFS関数について

バージョンを気にせず使える

数式が長くなりがちで少し混乱しやすい
ネストが最大で64個

それぞれメリットデメリットあります。様々なPCで操作する場合にはIF関数のほうが無難であると言えそうです。

AND？OR？

論理関数ではAND関数とOR関数というものもありますので併せて確認しておきましょう。

AND(論理式①,論理式②,…)
OR(論理式①,論理式②,…)
それぞれ、TRUEかFALSEで結果を返します。

日本語で条件のANDまたはORについて考えるならば
AND＝論理式①、論理式②のどちらも当てはまる
OR ＝論理式①、論理式②のどちらかが当てはまる
と読んでしまえばいいでしょう。ちなみにネストの数は無制限です。

すこし問題を使って考えてみましょう

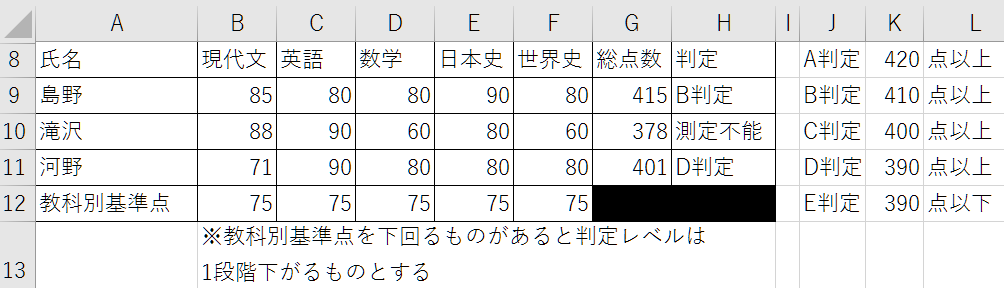
島野さん(H2セル)の判定結果は以下のようになっています。

=IFERROR(INDEX($J$8:$J$12,MATCH(IF(G9>=K$8,J8,IF(G9>=K$9,J$9,IF(G9>=K$10,J$10,IF(G9>=K$11,J$11,J$12)))),$J$8:$J$12,0)+IF(OR(B9<=B$12,C9<=C$12,D9<=D$12,E9<=E$12,F9<=F$12)=FALSE,0,1),1),”測定不能”)

例題でやったことの応用です。模試の総点数でA~Eの評価が決まりますが、今回は更に教科毎の点を評価に加味していて『教科別基準点をクリアしていればそのまま、1科目でも基準点以下なら5段階評価が1つ下がる』という数式です。
AND関数によって教科毎の点と基準点の比較を論理式として、どれも当てはまる(基準点クリアしている)ならTRUEになります。TRUEであれば0、FALSEならば1としてINDEX関数の高さに0または1が加算されます。
それによって、1段階評価が下がるかどうかを判別しているということになります。

これはOR関数を使っても同様のことができます。

『教科別基準点を1科目でも基準点以下なら5段階評価が1つ下がる(TRUE)』なのでFALSEならば0、TRUEならば1としてしまえばあとは同様です。(不等号の向きに注意)

論理関数は特に他の関数との組み合わせが多いので、IFS関数がというよりも如何に関数自体を組み合わせるかが重要になります。