中級者でも人によっては聞いたことがないかもしれないのが今回のPMT・PPMT・IPMT関数です。タイトルにも支払計算とありますが、ローンなどのシミュレーションに使える関数となっています。
難しい言葉は使わずに解説してみますので、実際に見てみましょう。
PMT・PPMT・IPMT関数とは？
整理して見やすい形にする
経過を見やすくする
今回は少し複雑な部分もあるので、ファイルを開きながら一緒に見ていくと理解が早いかもしれません。
PMT・PPMT・IPMT関数とは？
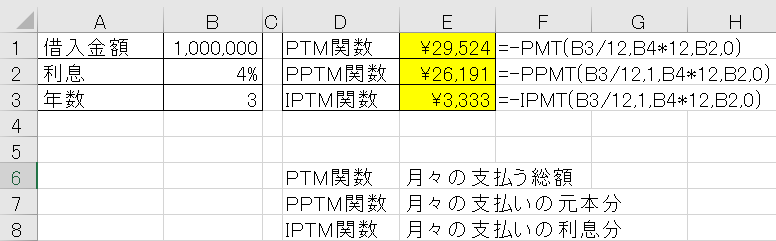
冒頭でも言いましたが、ローン(積立)の計算の計算に使います。それぞれの関数は以下のような関数です。
PMT関数 ：月々の支払(積立)金額合計を出す
PPMT関数：月々の支払金額の元金分
IPMT関数：月々の支払金額の利息分
以下の例でそれぞれを見ていきましょう。
PMT関数の数式
=PMT(利息,期間,現在価値,将来価値,支払期日)
利息は6%の1ヵ月分なのでB2/12、期間は3年なのでB3×12となります。
現在価値に関しては、ローンなどの借入の場合は借入金額、積立の場合は頭金(なしの場合は0)にします。
将来価値については、ローンなどの借入の場合は0、積立の場合は目標金額を入れます。
支払期日は月初かそれ以外かを選ぶことができ、月末の場合は0か省略、それ以外の場合は0以外の数字を入れます。
PPMT関数の数式
=PPMT(利息,期,期間,現在価値,将来価値,支払期日)
ほとんどPMT関数と似ていますが、利息の次に「期」の設定が必要です。「期」は何回目の支払ですか？という意味です。今回は3年の支払なので月々の支払回数なら3年×12回＝36回ありますが、それの何回目なのかに応じて利息と元金の割合が変わる為です。
なので「期」には該当する支払回数目を入れます。今回は1回目の支払の元金分を調べるために1とします。
IPMT関数の数式
=IPMT(利息,期,期間,現在価値,将来価値,支払期日)
PPMT関数とまったく同じです。利息の次に「期」の設定が必要です。PPMTでは支払額の元金部分を出しますが、IPMTでは利息がいくらにあたるのかを算出します。
なので「期」にはPPMTと同様、今回は1回目の支払の利息分を調べるために1とします。
ではそれぞれを計算してみましょう。
PMT関数＝PPMT関数+IPMT関数になっていますね。
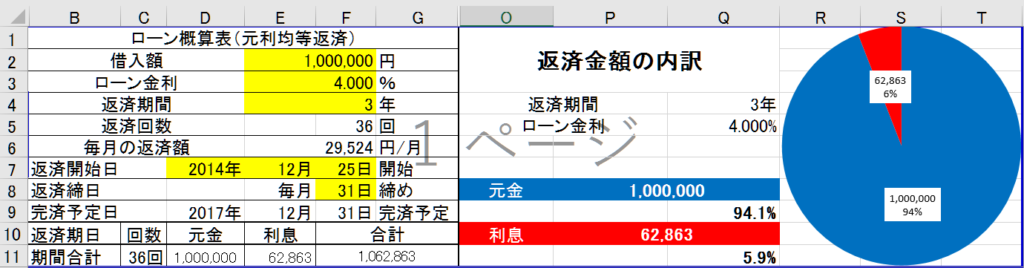
整理して見やすい形にする
どうせなら、見やすい形にしてみましょう。
月々の支払だけでなく、総額の元金と利息割合を一覧にして見れるのが重要です。また円グラフなどで視覚アプローチも有効です。他にも
- 完済時の年齢
- 上下に並べてパターン比較
- 家計簿と連動させてより正確なシミュレーション
こういった使い方もできるかと思います。サンプルファイルには家計簿をつけていますので、お好みに合わせて加工してみてください。
経過を見やすくする
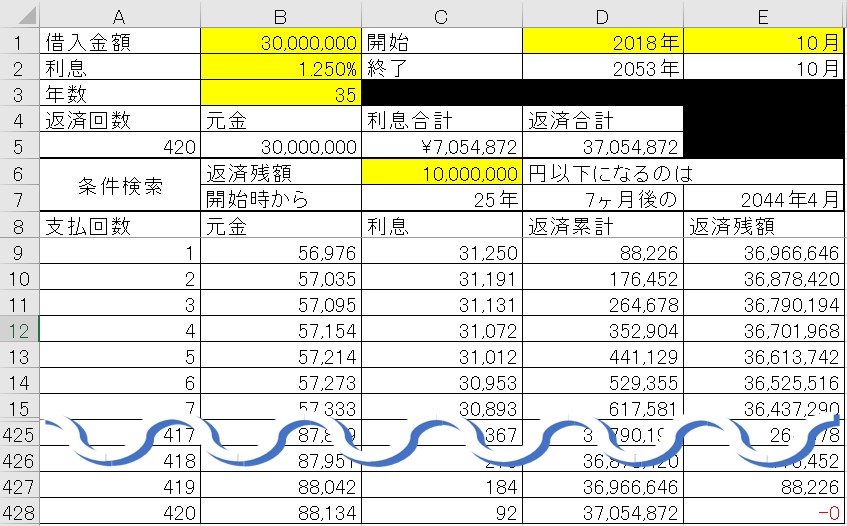
地味にですが、『一定の段階で支払残高がいくらあるのか』、『返済残高が○○円以下になるのはいつごろなのか』というのは住んでいる物件を売却して新しい物件の購入費用などに充てる意味などで非常に重要な視点になります。こちらを実装していきます。
表を順に解説していきますが、最初は8行目以下の推移表の部分です。今回は35年ローンで考えて420回まで表示する形にしています。
推移表の作成
支払回数の推移
=IF($A$5>=ROW(A1),ROW(A1),””)
これで必要分だけ支払回数が表示されます。
元金の推移
=IF(A9=””,””,-PPMT($B$2/12,$A9,$B$3*12,$B$1,0,0))
PPMT関数の数式の「期」を支払回数のセルにすれば回数ごとの元金割合がでます。
利息の推移
=IF(A9=””,””,-IPMT($B$2/12,$A9,$B$3*12,$B$1,0,0))
IPMT関数の数式の「期」を支払回数のセルにすれば回数ごとの利息割合がでます。
この段階でオートフィルで全回数の利息を算出できるので利息合計も出せます。借入金額と合わせれば最終的な返済金額合計を出すことができますね。
支払金額合計
=IF(A9=””,””,SUM(B9:C9))
1回目はこちらの数式にします。
=IF(A10=””,””,SUM(B10:C10)+D9)
2回目以降はこちらの数式で今回の支払分と前回までの支払=累計金額になります。
返済残高推移
=IF(A9=””,””,D$5-D9)
先程。返済残高合計が出ているのでそこから累計金額を引けば残高が出せます。
条件検索
返済残高が○○円以下になるのはいつかを調べます。
今回はC10セルを検索値にしています。
画像には載っていませんが、F9セルに
=IF(E9>=C$6,1,””)
このように入れます。
今回なら10,000,000以下なら空白、そうでなければ1と返します。これで10,000,000以下になるタイミングがわかりますね。1回支払回数が増えるごとに1ヵ月なので12回増えれば1年という計算です。
今回は306回なので1回目を1ヵ月として+1します。よってC10セルが
=ROUNDDOWN((COUNT(F9:F428)+1)/12,0)で25年になります。
※ROUNDDOWN関数は切捨ての関数で(値,少数点の位置)です。
D10セルは306÷12の余りが知りたいので
MOD((COUNT(F9:F428)+1),12)
としてあげます。
※MOD関数は余りを算出する関数で、(値、割る数)であまりが出てきます。
今回は307÷12＝25余り7になるので25年と7か月になります。
E10セルで開始から算出した年月を足しています。
=DATE(D1,E1,1)+(C7*365)+(D7*30)
厳密には1ヵ月30日ではないので誤差は発生しますが、1ヵ月以内なので無視しても大丈夫です。
ここまで組んでみるとだいぶローンについてある程度シミュレーションが出来るようになるのではないでしょうか？(固定金利の場合ですが…)
